大数2015年6月号の宿題を解く
☂
「大学への数学」2015年6月号の「宿題」のコーナーで、次のような問題が出ていました。
$m, n$は整数で、$m \geqq 0, n \geqq 1$とする。座標平面上の、$x$座標と$y$座標がともに1以上$n$以下の整数である$n^2$個の点からなる集合を$S$とする。以下の2条件を共に満たすように、$S$の各要素に0以上の整数値を割り当てる方法の総数を$m, n$で表せ。 (1) $S$の要素に割り当てられた値の総和は$m$である。 (2) 座標軸に平行な長さ1の線分を$2(n-1)$本組み合わせて$(1,1)$から$(n,n)$まで移動する最短経路$P$で、$P$上にある$S$の要素に割り当てられた値の和が$m$であるものが存在する。
今日は、この問題を考えてみます。記事の最後に、自分の解答を載せますが、そこに至るまでの試行錯誤も載せておきます。解答だけだと突然いろんなことが出てきて意味不明だと思うのですが、途中の試行錯誤も読むと、あら不思議、やっぱり意味不明です。もっとすっきりしたわかりやすい解答がきっと8月号に載るのでしょう。ちなみに、この「宿題」の解答期限は過ぎているので、この解答を書いて応募しても意味ないです(正解の保証もありません)。
普段このブログは888文字で書いていますが、今日は8888文字のロングバージョンです。
【目次】
読む
まず、状況がよくわからないので、条件(2)をよく読むところから始めます。「座標軸に平行な長さ1の線分」っていうのは、「縦か横に1ずつ移動して」ってことですね。格子状の道の上を移動する、「場合の数」でよくでてくるシチュエーションです。言葉だけで書くと、こんなにめんどくさくなるんですね。
「最短経路$P$上にある$S$の要素に割り当てられた値の和が$m$である」とは、よく考えると、「最短経路$P$は、正の数を割り当てた点を全部通る」ってことです。
結局、「正の数を割り当てた点を全部通る最短経路が存在する、そんな割り当て方は何通り?」ってことですね。
実験する
で、求める対象がわかったけれど、「じゃあそれどうやって数えるの?」ってところが、まだわかりません。ぱっと思いついた方針は、「まず最短経路を考えて、その最短経路上の点に$m$を振り分ける、って考えればいいんじゃね?」ですね。単純に「最短経路の数×$m$の振り分け方の数」でいけるんじゃないか、と。まぁ、そんな簡単なはずはないのですが、とりあえず、簡単な例で結果がどうなるか実験してみましょう。
まずは、$n=2,m=2$というシンプルな場合を考えてみます。このとき、(1)のみを満たす割り当て方は、次のように全部で10通りあります。
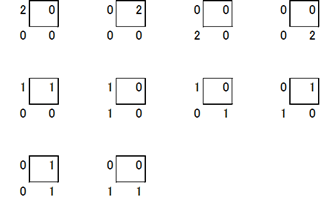
左下の(1,1)から右上の(2,2)へ行く方法を考えると、「上⇒右」と行くか、「右⇒上」といくしかありません。このとき、条件(2)を満たさないものは、左上と右下、つまり、(1,2)と(2,1)に1を割り振っているものですね。これだけが条件(2)を満たさず、他の割り当ては満たします。つまり、この場合、条件を満たすものは、9通りですね。
さて、上で書いた方針「最短経路の数×$m$の振り分け方の数」を考えてみましょう。最短経路の数は、先ほど書いたように、2通りしかありません($_2\mathrm{C}_1$通りです)。一方、$m$の振り分け方はどうなるでしょうか。
3ステップでゴールしますが、この3つの点に合計が2になるように数字を振り分けることを考えます。どこかに2が入る方法は3通り、1が2回入る方法は3通り。なので、全部で6通りですね。
すると、「最短経路の数×$m$の振り分け方の数」は、2×6で12通り。あれ? おかしいです。正解の9通りでないどころか、そもそも条件(1)だけを満たす10通りより多くなってしまいました。
間違える
よく考えると、「最短経路の数×$m$の振り分け方の数」という求め方では、同じ結果をダブって数えてしまうことになるんですね。例えば、「上⇒右」という時計回りの経路に対し、1つ目と3つ目に1を割り当てるとします。また、「右⇒上」という反時計回りの経路に対し、1つ目と3つ目に1を割り当てると、結果が同じになってしまいます。どちらも、(1,1)と(2,2)に1を割り当てるという結果になります。こうしたダブりがあるので、全体の10通りよりも多くなってしまったんですね。
上の場合、(1,2)に割り当てられた数字は0ですが、最短経路上にないから0なのか、最短経路上にあったけど0が割り当てられたのか、後になってから見分けることができません。つまり、最短経路をはじめに指定しても、「0」の割り当て方によっては、最短経路の一意性が崩れてしまうことがある、ということです。なので、最短経路を切り口に考えるのは無理そうです。
この後、具体的に割り当て方を書き出していくと、$n=3,m=2$のときは36通り、$n=3,m=3$のときは100通りであることがわかりました。このことから、答えは何かの2乗かな、っていう予想が生まれました。しかし、どうやって数えるかは、一から考え直しです。
計算する
次に考えたのは、「0以外が割り当てられた点のうち、ゴールに一番近いもので場合分けする」というものです。最初に考えていた方法では、0を割り当てた点がやっかいでした。なので、はじめから「0がないところ」に着目すればいいんじゃないか、という発想です。ちなみに、ゴールからの距離が等しいのに、0以外が割り当てられる、ということはありません。もしそんなことがあれば、正の数が割り当てられた点を全部通る最短経路が存在しなくなってしまいます(最短経路は、1歩進むごとにゴールに近づかないといけないので、ゴールから同じ距離の点は1回しか通らない)。
さて、$m$を正として、こういうものを考えます。問題文の点$(n,n)$を点$(i,j)$に変え、条件(1)(2)と同様の条件を満たす割り当てを考える。このうち、点$(i,j)$に割り当てた数字が0でない割り当て方を$C(i,j,m)$と書く、と。このとき、求めるものは、
\begin{eqnarray}
\sum_{i\leqq n} \sum_{j\leqq n} C(i,j,m)
\end{eqnarray}
となります。突然意味不明な式ですが、これは条件を満たす割り当てを「最後に正の数字が割り当てられた点」で場合分けしているにすぎません。
また、$C(i,j,m)$は、$(i,j)$の値によって、次のようにわけることができます。
\begin{eqnarray}
C(i,j,m) = 1+\sum_{(p,q)\in S_{ij}} \sum_{1\leqq r\leqq m-1} C(p,q,r)
\end{eqnarray}
ここで、$S_{ij}$は、$x$座標が$i$以下の正の整数、$y$座標が$j$以下の正の整数で、$(i,j)$を除いた点の集合とします。これは、$(i,j)$が$m$ならそれ以外の点全部に0を割り当てるしかないので1通り、$m-r$なら、$(i,j)$に来るまでの間に合計が$r$にならないとダメで、それについても「最後に正の数字が割り当てられた点」で場合分けして足し合わせればいい、ということです。
まぁこう書いてみたものの、この計算どうやってやるんだっていう重大な問題があります。とりあえず、小さい値に対して計算してみて、なにかきれいな形になったらうれしいなぁ、と妄想してみます。ゴリゴリ計算すると、次のことがわかります。
\begin{eqnarray}
C(1,1,m)&=&1 \
C(1,2,m)&=&C(2,1,m)=m \
C(2,2,m)&=&m^2 \
C(1,3,m)&=&C(3,1,m)=\frac{1}{2}m(m+1) \
C(2,3,m)&=&C(3,2,m)=\frac{1}{2}m^2(m+1) \
C(3,3,m)&=&\frac{1}{4}m^2(m+1)^2 \
\end{eqnarray}
これらを使って、$n=3$のときに、求める総数を出すと
\begin{eqnarray}
\frac{1}{4}(m+1)^2(m+2)^2 \
\end{eqnarray}
となります。省略してますが、計算はすごく大変です。Σの計算がたくさん出てきてしまいます。これを一般の$n$でやるのは無理です。$n$についての数学的帰納法という手もありますが、計算がごつすぎます。
ちなみに、$m=3$としてみると100通りとなり、具体例で計算した時と答えはあっているようです。また、この式は、$({}{m+2} \mathrm{ C }{2})^2=({}{m+2} \mathrm{ C }{m})^2$とも書けるので、答えは$({}{n+m-1} \mathrm{ C }{m})^2$なのかな、という予想が生まれます。
この予想から、「何から何を選べば答えになるんだ?」という逆からの発想も狙いつつ、まだまだ試行錯誤します。
近づく
上では$n$を順番に大きくしてきましたが、次は、1xnからはじめてnxnを考えてみようと思いました。つまり、正方形を大きくしていくんじゃなくて、長方形を横に広げて正方形にしていくイメージです。なぜ1xnなんて考えだしたかというと、この場合は経路のことを考えてすむからです。
![]()
$(1,1)$から$(1,n)$までの点に$m$を割り当てる方法を考えます。この場合、最短経路は1本しかないので、合計が$m$になるような割り当てだけ考えればいいです。
次のような状況を考えましょう。ボールを$n+m$個用意し、横一列に並べます。次に、ボールの間($n+m-1$箇所)から$n-1$箇所を選んで区切りを入れ、$n$グループに分けます。左から$i$番目のグループのボール数から1引いたものを、$(1,i)$に割り当てます。すると割り当てた数の合計は$m$になります。また、ボールの分け方と数字の振り分け方は、1対1に対応します。
なので、このときの場合の数は、${}{n+m-1} \mathrm{ C }{n-1}={}{n+m-1} \mathrm{ C }{m}$となります。おっと、この形、上で予想した答え$({}{n+m-1} \mathrm{ C }{m})^2$と繋がっている気がします。答えに近づいてる感!
ただ、$(1,1)$から$(2,n)$までの点に合計が$m$になるように割り当てる方法になると、やはりつまってしまいます。0じゃないところで場合分けをしないとダブってしまうので、結局前にやったえげつない計算へと向かってしまいます。
計算をゴリゴリやるか。とも思ったのですが、$(1,1)$から$(1,n)$の場合をよくよく見てみます。この答えにつながっている感じを放っておくのはもったいない気がします。
そもそも、${}{n+m-1} \mathrm{ C }{m}$とはなんでしょう。今取り組んでいるような、経路問題でもよく見る形です。ん? これは、次の図で左下から右上に行く最短経路数と同じじゃないか?
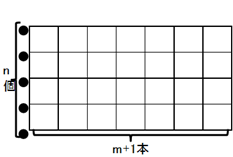
上に$n-1$、右に$m$移動することを考えると、確かにこの答えになります。しかし、これは$(1,1)$から$(1,n)$へ行く場合だから横に平面の形で描けたけど、$(1,1)$から$(n,n)$の場合にはどうすれば。。。あ!
ひらめく
なるほど。次元を一個あげるんですね。この問題は、$(1,1)$から$(n,n)$への最短経路を考える問題ではなかったんです。$(1,1,0)$から$(n,n,m)$への最短経路を考える問題だったのです。
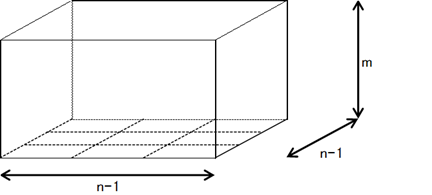
$(1,1,0)$から$(n,n,m)$への最短経路を上から見ると、もちろんそれは$(1,1)$から$(n,n)$への最短経路になっています。そして、上に上がった回数が、その点に割り当てられた数に対応するわけです。なるほど、この問題はそういう意味なんですね。
ただ、まだどうやって数えればいいかわかりません。$(1,1,0)$から$(n,n,m)$への最短経路と関連があるのは予想できますが、求めるものと1対1になっているわけではありません。
例えば、(1,1,0)から(2,2,2)へ行く場合、まず上に行き、また最後にも上に行ったとした場合、(1,1,1)から(2,2,1)へ行く方法は、上から見たときに時計回りと反時計回りの2種類あります。以前見たダブりの例と全く同じダブり方をしています。
うーん、とうなりながら、図の奥行の$n-1$と高さの$m$をぼーっと見ていました。すると、あるとき、ピカッとひらめきました。「そうか、横から見るんだ!」
上の例で、時計回りでも、反時計回りでも、前から見た経路、横から見た経路は変わりません。つまり、最短経路のうち、前から見た経路、横から見た経路が異なるものだけをカウントすればいいんじゃないか、と予想できます。
もしそうだとすると、横に$n-1$、縦に$m$移動する最短経路を2つ選ぶ場合の数を求めることになるので、答えは$({}{n+m-1} \mathrm{ C }{m})^2$。これは前に考えていた予想と一致します。答えはこれに違いない!
解答する
今ひらめいたことを確認しつつ、答案に書くことを考えていきます。が、ちょっと書きづらいです。直感的には、前からと横から見た経路を考えればいいのですが、そのイメージで答案に落としていく力が僕にはありません。
そこで、こういうことを考えます。「(0,1)から(0,n)、(1,0)から(n,0)に合計が$m$になるように数字を割り当て、そこから条件を満たす割り当てを考える」と。
条件を満たす割り当て方は、次のようにすればいいです。(1,1,0)から(n,n,m)に行くことを考えます。このとき、(0,1)から(0,n)、(1,0)から(n,0)に割り当てた数字に対し、(x,0)と(0,y)が正になっている箇所は上に進む、と。これを原点に近い方から順番にやっていきます。
そうすれば、できあがる経路は、(1,1,0)から(n,n,m)への最短経路になります。上から見たとき、上に上がってきた数字を割り当てれば、条件を満たすことはわかります。
解答を書くには、この方針でいけるはずですが、この場合、3つのことを書かないといけないでしょう。
1つ目は、こうして作った割り当て方が、条件を満たすこと。
2つ目は、こうして作った割り当て方が、他のものとかぶらないこと。
3つ目は、こうして作った割り当て方以外に、条件を満たすものがないこと。
1つ目は、ちゃんと目的のものに対応しているかどうかの確認です。また、数学チックに言うと、2つ目は単射であること、3つ目は全射であることです。これを確認しないと、「(0,1)から(0,n)、(1,0)から(n,0)に合計がmになるように数字を割り当てる場合の数」が求めるものだということができません。
以上のことをくどくど書いてまとめたものが、次の解答になります。解答を書く方針は、直観的に理解した「3次元の最短経路を、前と横から見る」をベースに書いていけばいいのですが、厳密に書くには少しトリッキーな書き方になってしまいます。いきなりこの答案を思いつくのは無理ですが、今までの試行錯誤を踏まえれば、突拍子さは軽減しているんじゃないかと思います。
直感的にわかったことをそのまま答案にできれば、もっと簡単に書けるはずなんですが。
【解答案】
$m=0$のとき、条件を満たすには、$S$の全要素に0を割り当てるしかないので、割り当て方は1通り。
$m\geqq 1$とする。各項が0以上の整数で、$\Sigma a_i^{(0)}=m$を満たす、項数$n$の数列${a_i^{(0)}}$を考える。
\begin{eqnarray}
A_1 &=& \min { i \mid a_i^{(0)} \gt 0 } \
a_i^{(1)}
&=&
\begin{cases}
a_i^{(0)} - 1 & ( i = A_1 ) \
a_i^{(0)} & ( i \ne A_1 )
\end{cases}
\end{eqnarray}
として、$A_1$と新しい数列${a_i^{(1)}}$を作る。以下、同様の操作をして、$A_1, \cdots , A_m$と${a_i^{(1)}}, \cdots, {a_i^{(m)}}$を作る。作り方から明らかに$A_1\leqq A_2 \leqq \cdots \leqq A_m$が成り立つ。また、$A_j=i$となる$j$の個数が$a_i^{(0)}$個となることも、作り方からわかる。
各項が0以上の整数で、$\Sigma x_i^{(0)}=\Sigma y_i^{(0)}=m$となる項数$n$の2つの数列${x_i^{(0)}}, {y_i^{(0)}}$を考える。これらに対し、上の操作で得られる$A_1, \cdots , A_m$を、それぞれ$X_1,\cdots, X_m$と$Y_1,\cdots, Y_m$とおく。
$S$の全要素に0を与えた後、各$(X_i,Y_i)$の値を1ずつ増やす$(i=1,\cdots, m)$。こうすれば、$S$の要素に割り当てられた値の総和は$m$になる。
$X_1\leqq X_2 \leqq \cdots \leqq X_m$と$Y_1\leqq Y_2 \leqq \cdots \leqq Y_m$が成り立つから、$(1,1)$から$(n,n)$までの最短経路で、すべての$(X_i,Y_i)$を通るものが存在する。
よって、${x_i^{(0)}}, {y_i^{(0)}}$から条件(1)(2)を満たす割り当てを作ることができる(※1)。このように、数列から割り当てを作る方法を、操作Aと呼ぶことにする。
操作Aにより得られた割り当てに対し、点$(i,j)$に割り当てられた値を$V(i,j)$で表す。このとき$\sum_j V(i,j)$は、$X_j=i$となる$j$の個数と一致する。よって、次が成り立つ。
\begin{eqnarray}
x_i^{(0)} &=& \sum_j V(i,j) \
y_i^{(0)} &=& \sum_j V(j,i)
\end{eqnarray}
このことから、${x_i^{(0)}}$や${y_i^{(0)}}$が異なれば、操作Aで得られる割り当ても異なることが分かる(※2)。
次に、条件(1)(2)を満たす割り当てがあったとする。点$(i,j)$に割り当てられた数字を$U(i,j)$で表すとし、
\begin{eqnarray}
x_i^{(0)} &=& \sum_j U(i,j) \
y_i^{(0)} &=& \sum_j U(j,i)
\end{eqnarray}
とする。このとき操作Aにより、${x_i^{(0)}}, {y_i^{(0)}}$から新しく割り当てを作ることができる。点$(i,j)$に新しく割り当てられた数字を$V(i,j)$で表すとする。
$U$と$V$が異なるとすると、次を満たす$k$が存在する。
\begin{eqnarray}
k=\min { i \mid U(X_i,Y_i) \ne V(X_i,Y_i) }
\end{eqnarray}
操作Aの定義から、$U(X_k,Y_k) \lt V(X_k,Y_k)$なので、次が成り立つ。
\begin{eqnarray}
\sum_{j\gt Y_k} U(X_k,j) \gt 0 \
\sum_{j\gt X_k} U(j,Y_k) \gt 0 \
\end{eqnarray}
しかし、これは、$x=X_k$上と$y=Y_k$上で正の整数が割り当てられた点を通る最短経路がないことを示すので、$U$の割り当て方は条件を満たさない(※3)。
以上から、
・操作Aにより、条件を満たす割り当てを与えることができること(※1)
・操作Aでは、初期値を変えれば、得られる割り当て方も変わること(※2)
・操作Aで作られるもの以外の割り当ては、条件を満たさないこと(※3)
が示された。
よって、求めるものは、各項が0以上の整数で、$\Sigma x_i=\Sigma y_i=m$となる項数$n$の2つの数列${x_i}, {y_i}$の与え方に一致する。
次の状況を考える。$n+m$個のボールを左右に一列に並べる。$n+m-1$箇所の隙間から$n-1$箇所を選んで区切りを入れ、ボールを$n$グループに分ける。このとき、左から$i$番目のグループにあるボールの数から1減らしたものを、$x_i$として、項数$n$の数列${x_i}$を作る。このとき、この数列は各項が0以上の整数で、$\Sigma x_i=m$を満たす。また、ボールの区切り方と数列の種類は、1対1に対応する。
よって、求める総数は、$({}{n+m-1} \mathrm{ C }{n-1})^2=({}{n+m-1} \mathrm{ C }{m})^2$となる。これは、$m=0$のときも成り立つ。よって、$({}{n+m-1} \mathrm{ C }{m})^2$が求めるものとなる。(終)