大数2015年9月号の宿題を解く

「大学への数学」2015年9月号の宿題コーナーで、次のような問題が出ていました。

【問題】 1から2015までの番号がつけられた2015本のひもがある。4030個の端を無作為に2つずつ2015個の組に分け、組になった端どうしをすべて結ぶことで、いくつかの輪を作る。このとき、ひも2015を含む輪が、ひも1、ひも2、・・・、ひも27をいずれも含まない確率を求めよ。

解答締切が過ぎたので、自分の解答を書いてみます。いつも書いている文字数におさまる短さで書けました。

[解答]
27+n本のひも（nは自然数）に対して問題文同様に輪を作る。「ひも28を含む輪が、ひも1からひも27のいずれも含まない」事象を事象Aとし、事象Aの起こる確率が1/55となることを示す。ひも28の片端に印をつけて片端Xとし、Xがどの端と結ばれるかに着目する。問題文より、Xが各端と結ばれる確率はそれぞれ等しい。

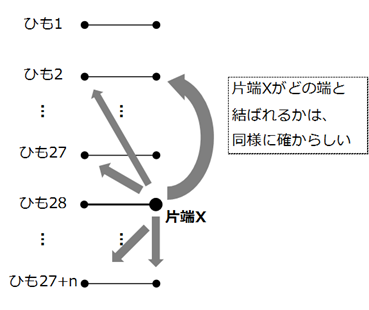
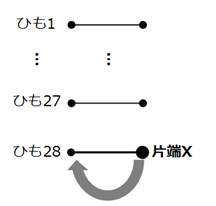
n=1のとき、片端Xは、残りの端55か所のうち、ひも28の反対側と結ばれるしかない。よって、事象Aが起こる確率は、1/55。

n=kのとき、事象Aの起こる確率が1/55とする。n=k+1のとき、事象Aは、片端Xが、ひも28のもう片端か、ひも29からひも28+kのどれかと結びつく場合に分けられる。

前者が起こる確率は、1/(2k+55)。また、このとき必ず事象Aが起こる。

後者の場合、片端Xと結びついたひものもう片端を新しく片端Xとみなせば、n=kの場合に帰着される。

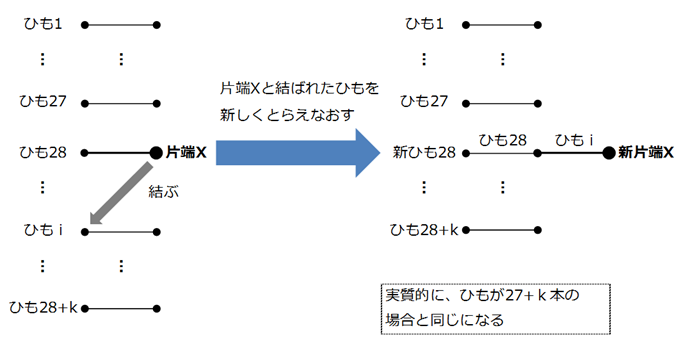
Xがひも29からひも28+kのどれかと結びつく確率は、2k/(2k+55)なので、仮定から、事象Aが発生する確率は、2k/(2k+55)×1/55となる。

よって、事象Aの起こる確率は、1/(2k+55) + 2k/(2k+55)×1/55 = 1/55となる。

以上から、事象Aが起こる確率は、1/55。2015本のひもに対し、ひも28ではなくひも2015について考えても同じなので、求める確率は、1/55となる。

[解答終わり]

結局、ひもが増えても、確率は変わりません。「自分自身か禁止されたひもを選ぶか」の確率に帰着されるんですね。不思議！