東京五輪新エンブレムが市松模様に決まったから、市松模様に関する数学の問題を書いてみるよ

これを読みました。

東京五輪 新エンブレム 市松模様の「作品Ａ」に決定 | NHKニュース

東京五輪のエンブレムはたくさん騒動があって、いろいろと残念な展開になっていましたね。人によっては、「もうこの話題はおなかいっぱいだよ」という意見の人もいそうです（僕も含む）が、まぁ、とりあえず決まってよかったですね。

「市松模様」と言えば、数学の問題でテクニックとしてたまに使われることがあります。めちゃくちゃ関連が薄いけど、書いてみますか。

【問題】
下のような４×４のマスで、左下のスタートから右上のゴールに移動する方法を考えます。ただし、上下左右のどちらかに１マスずつしか動けないとします。このとき、すべてのマスを１度だけ通ってゴールする方法がないことを示しなさい。

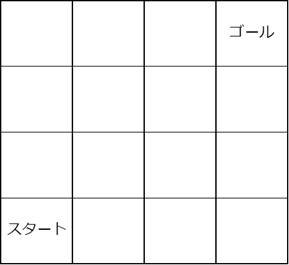
試しに何度かやってみるとわかるんですが、確かにすべてのマスを通って右上に行く方法はなさそうなんですよね。でも、「オレはできなかった」は、できないこと、存在しないことの証明にはならないんですよね、残念ながら。

もちろん、全パターンを調べ上げるという力技もありますが、もう少し楽をしましょう。冒頭の予告通り、市松模様を使います。次のようにマスを塗っていきます。

スタートを黒にし、白黒交互に、市松模様になるように塗っていきます。すると、ゴールは黒になり、スタートと同じ色になります。

ここまでだと、まだ何のことだかわかりませんね。市松模様にすることで何がいいのかというと、「１マス進むと色が変わる」ことが利用できる点なんですよね。

どういう経路をたどったとしても、マスの色は「黒白黒白黒白…」というように、黒と白が交互になっていきます。もしすべてのマスを１回ずつ通ったとすると、16個のマスを通ったことになります。黒と白は交互なので、16マス目の色は「白」でないといけません。しかし、ゴールのマスは黒なんですよね。なので、「16マス目でゴールする」ことはできません。

ということで、このことから「すべてのマスを1度だけ通ってゴールする方法はない」ということが分かります。市松模様にするだけで、問題が解けるようになるのはおもしろいですね。